《数字图像处理》– 冈萨雷斯 读书笔记
背景知识
前言
- 对分割区域加以表示与描述,以便使“自然状态的”像素更适合计算机处理。
- 表示区域设计到两个基本选择
- 用外部特征(区域的边界)表示区域
- 用内部特征(组成区域的像素)表示区域
背景
单元数组与结构
单元数组
不同类型的元素可以放在一个数组中
单元数组的简单说明
自己写一个函数 image_stats
该函数用来输出一幅图像的平均亮度、维数、行的平均亮度和列的平均亮度,则可以使用“标准”方法写函数
12345function [AI, dim, AIrows, AIcols] = image_stats(f)dim = size(f);AI = mean2(f);AIrows = mean(f, 2);AIcols = mean(f, 1);若使用单元数组,则可以改成:
12345function G = image_stats(f)G{1} = size(f);G{2} = mean2(f);G{3} = mean(f, 2);G{4} = mean(f, 1);其中 G(1) = {size (f)} 合法
单元数组也可以是多维的
12345function H = image_stats2(f)H(1, 1) = {size(f)};H(1, 2) = {mean2(f)};H(2, 1) = {mean(f, 2)};H(2, 2) = {mean(f, 1)};同理,此处也可写成 H{1, 1} =size(f)
额外的维数可以按照类似的操作
结构
结构的简单说明
12345function s = image_stats(f)s.dim = size(f);s.AI = mean2(f);s.AIrows = mean(f, 2);s.AIcols = mean(f, 1);其中s 是一个结构,s本身是一个标量,它与本例中的4个域相关。
参数为图片时
12345678function s = image_stats(f)K = size(f);for k = 1:K(3)s(k).dim = size(f(:, :, k));s(k).AI = mean2(f(:, :, k));s(k).AIrows = mean(f(:, :, k), 2);s(k).AIcols = mean(f(:, :, k), 1);end
MATLAB 和 IPT 函数
函数imfill
该函数对于二值图像和灰度图像的作用不同
1gB = imfill(fB, locations, conn)在输入二值图像 fB 的背景像素上从参数locations指定的点开始,执行填充操作。
1gB = imfill(fB, conn, 'holes')1g = imfill(fI, conn, 'holes')将填充输入灰度图像fI 的孔洞
函数find 可以和 bwlabel一起使用,返回构成某个指定对象的像素的坐标向量。
1[gB, num] = bwlabel(fB)产生了多个连续区域(即num > 1)
则使用一下语法可以获得第二个区域的坐标:
1[r, c] = find(g == 2)
函数sortrows
对数组进行排序
1z = sortrows(S)S 必须是矩阵或列向量
函数unique
既对数组进行排序,又去除重复行
1[z, m, n] = unique(S, 'rows')函数circshift
对数组进行向上、向下或侧移指定位置数的移位操作
1z = circshift(S, [ud lr])ud 是 S 向上 或向下移位的元素数
若S 是一幅图像,则circshift 就是对图像进行的卷动操作或平移操作。
基本的M函数
函数boundaries
输出的B是一个单元数组,其元素是已找到的边界的坐标
计算出每个边界中的第一个点和最后一个点
1B = boundaries(f, conn, dir)或者
1B = boundaries(f)1234B = boundaries (f);d = cellfun('length', B);[max_d, k] = max(d);v = B{k(1)};
函数bound2eight
会从上一个函数的基础上移除一些像素
1b8 = bound2eight(b)函数bound2four
同bound2eight
函数bound2im
1g = bound2im(b, M, N, x0, y0)生成一幅二值图像g ,参数 x0 y0 决定图像中b 的最小x 和y 坐标位置
函数bsubsamp
1[s, su] = bsubsamp(b, gridsep)输出s 是一个比b有更少的点的边界,点的数目由gridsep的值确定,su 是按比例取得的边界点的集合,这样可使坐标的转换趋于一致。
函数connectpoly
1z = connectpoly(s(:,1), s(:, 2))当对边界进行二次取样时,用此函数将图像的点重新连接起来
s 是二次取样后的边界的坐标
函数intline
1[x, y] = intline(x1, x2, y1, y2)当对边界进行操作时,计算连接两点的一条直线的整数坐标。
表示
链码
Freeman链码
函数fchcode
1c = fchcode (b, conn, dir)该函数计算一个保存在数组b中的np*2 个已排序边界点集的Freeman链码
Freeman链码及其某些变体
1234567891011121314>> h = fspecial('average', 9);>> g = imfilter(f, h, 'replicate');>> g = im2bw(g, 0.5);>> g = im2bw(g, 0.5);>> B = boundaries(g);>> d = cellfun('length', B);>> [max_d, k] = max(d);>> b = B{k};>> [M N] = size(g);>> g = bound2im(b, M, N, min(b(:, 1)), min(b(:, 2)));>> [s, su] = bsubsamp(b, 50);>> g2 = bound2im(s, M, N, min(s(:, 1)), min(s(:, 2)));>> cn = connectpoly(s(:, 1), s(:, 2));>> g2 = bound2im(cn, M, N, min(cn(:, 1)), min(cn(:, 2)));
使用最小周长多边形的多边形近似
MPP方法
寻找MPP方法的基础
- 对应一个简单连接的细胞联合体的MPP是本身不相交的。令P表示该MPP。
- P的每一个凸顶点与一个黑点 相符
- P的每一个凹顶点与一个白点相符
- 若一个黑点为P的一部分,且不是P的凸顶点,则其在P的边缘上
查找一个区域的 MPP 的如下步骤:
- 获取细胞联合体
- 获取细胞联合体的内部区域
- 使用函数 boundaries 以4 连接顺时针坐标序列的形式获得步骤2 中的区域的边界
- 使用函数 fchcode 获得该4 连接序列的Freeman 链码
- 从链码中获得凸顶点与凹顶点
- 使用黑点作为顶点构造一个初始多边形,在进一步的分析中删除位于该多边形之外的任何白顶点
- 用剩余的黑白点作为顶点构造一个多边形
- 删除所有为凹顶点的黑点
- 重复步骤7 和8 ,直到变化停止,此时,所有角度为180 ° 的顶点均将删除,剩下的点就是MPP的顶点
MPP算法实现总用到的一些M函数
函数qtdecomp
1Q = qtdecomp(B, threshold, [mindim maxdim])Q 是一个包含四叉树结构的稀疏矩阵,若Q (k, m)非零,则
(k, m)非零,则(k, m)为分解中的坐上块,块的大小为Q(k, m)
函数qtgetblk
1[vals, r, c] = qtgetblk(B, Q, mindim)vals 是一个在B 的四叉树分解中包含 mindim * mindim 个块的值的数组,而Q 是由函数qtdecomp返回的稀疏矩阵,参数r 和c 是包含左上角的行和列坐标的向量
函数inpolygon
1IN = inpolygon(X, Y, xv, yv)X 和 Y 是包含待测点的x 和y 坐标的向量,而xv 和yv是包含按顺时针和逆时针顺序安排的多边形顶点的x 和y 坐标的向量
函数minerpoly
1[x, y] = minperpoly(B, cellsize)B是一个二值图像,它包含单个区域或边界,而cellsize 是细胞联合体中用于形成边界的方形单元的大小
使用minerpoly函数的实例
123456789101112131415161718b = boundaries(B, 4, 'cw')b = b{1};[M, N] = size(B);xmin = min(b(:, 1));ymin = min(b(:, 2));bim = bound2im(b, M, N, xmin, ymin);[x, y] = minperpoly(B, 2);b2 = connectpoly(x, y);B2 = bound2im(b, M, N, xmin, ymin);[x, y] = minperpoly(B, 3);b3 = connectpoly(x, y);B3 = bound2im(b, M, N, xmin, ymin);[x, y] = minperpoly(B, 4);b4 = connectpoly(x, y);B4 = bound2im(b, M, N, xmin, ymin);[x, y] = minperpoly(B, 8);b8 = connectpoly(x, y);B8 = bound2im(b, M, N, xmin, ymin);
(a)是原图像、(b) 4 连接边界 、(c) 使用大小为2 的方形边界单元获得的MPP、(d) ~(f)分别使用大小为 3, 4和 8 的方形单元获得的MPP
标记
标记是边界的一维函数的表示,它可以通过多种方法生成。
函数signature
可用于查找给定边界的标记
1[st, angle, x0, y0] = signature(b, x0, y0)函数cart2pol
函数signature 使用函数 cart2pol 将笛卡儿 坐标转换为极坐标
1[THETA, RHO] = cart2pol(X, Y)函数pol2cart
将极坐标转换为笛卡儿坐标
1[X, Y] = pol2cart(THETA, RHO)边界片断
将一条边界分解为片断通常是很有用的。
分借降低了边界的复杂度,从而简化了描述过程
这里用函数regionprops处理
骨骼
用于表示平面区域结构形状的一种重要方法是将其简化为一幅图形,这一简化可以通过一种细化(也称骨骼化)算法获取区域骨骼来完成。
函数bwmorph
该函数用来生成二值图像中所有区域的骨骼
1s = bwmorph(B, 'skel', Inf)1234567>> f = im2double(f);>> h = fspecial ('gaussian',25,15);>> g = imfilter(f, h, 'replicate');>> g = im2bw(g, 1.5*graythresh(g));>> s = bwmorph(g, 'skel', Inf) ;>> s1 = bwmorph(s, 'spur', 8);>> s2 = bwmorph(s1, 'spur', 7);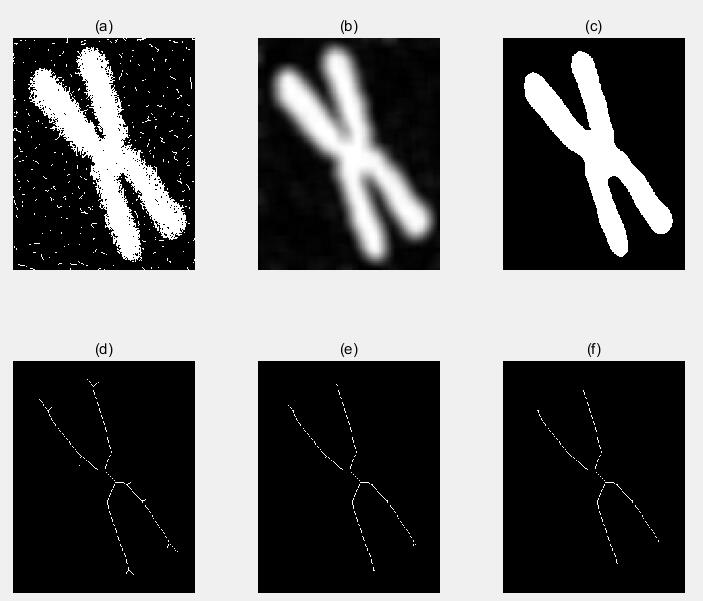
(a) 分割后的人类染色体
(b) 使用 25 *25 高斯空间掩模(sig = 15)平滑原图像的结果
(c)经阈值处理后的图像
(d) 骨骼
(e) 应用8 次去除毛刺的算法后的图像
(f)再应用7次去除刺算法后的骨骼